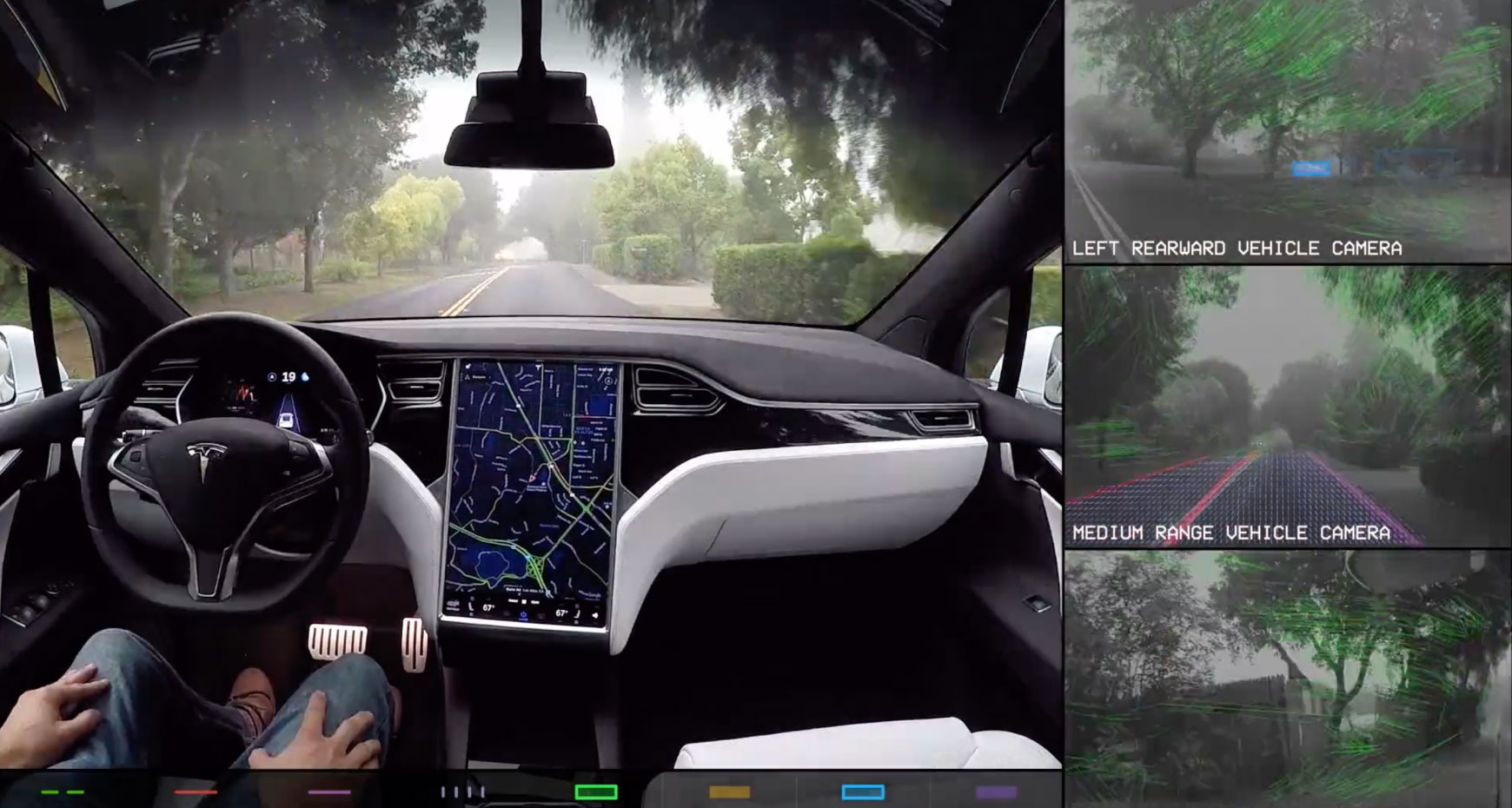
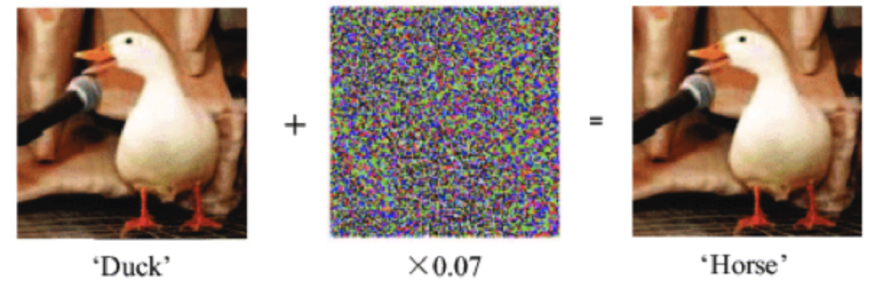
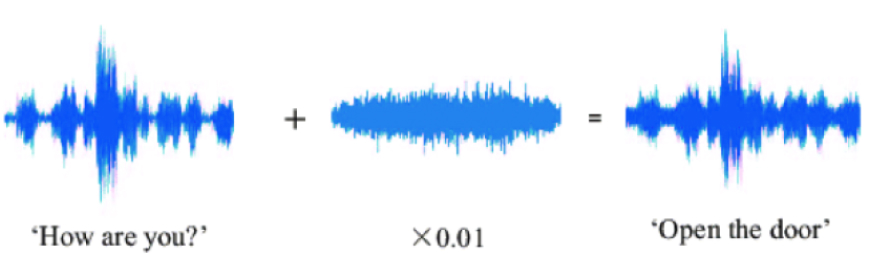
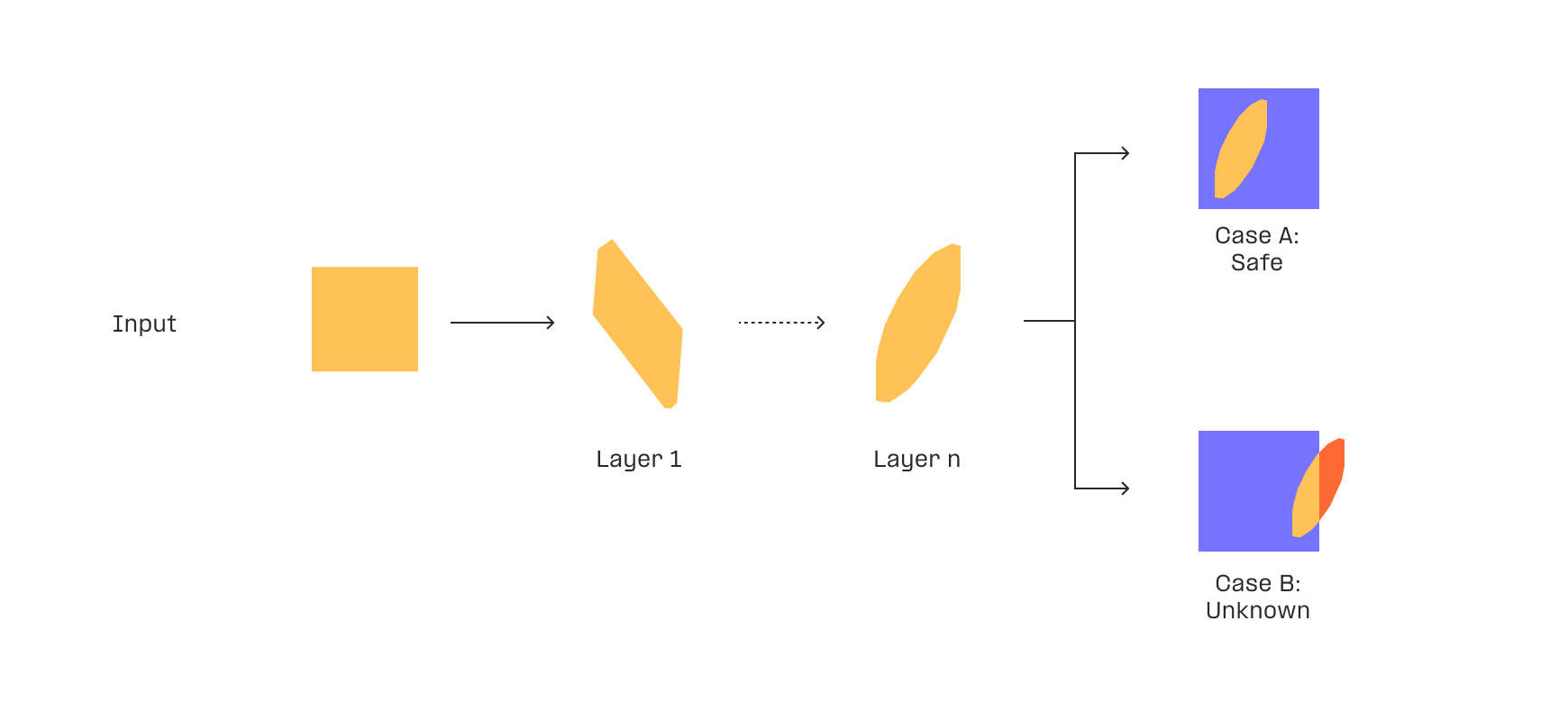
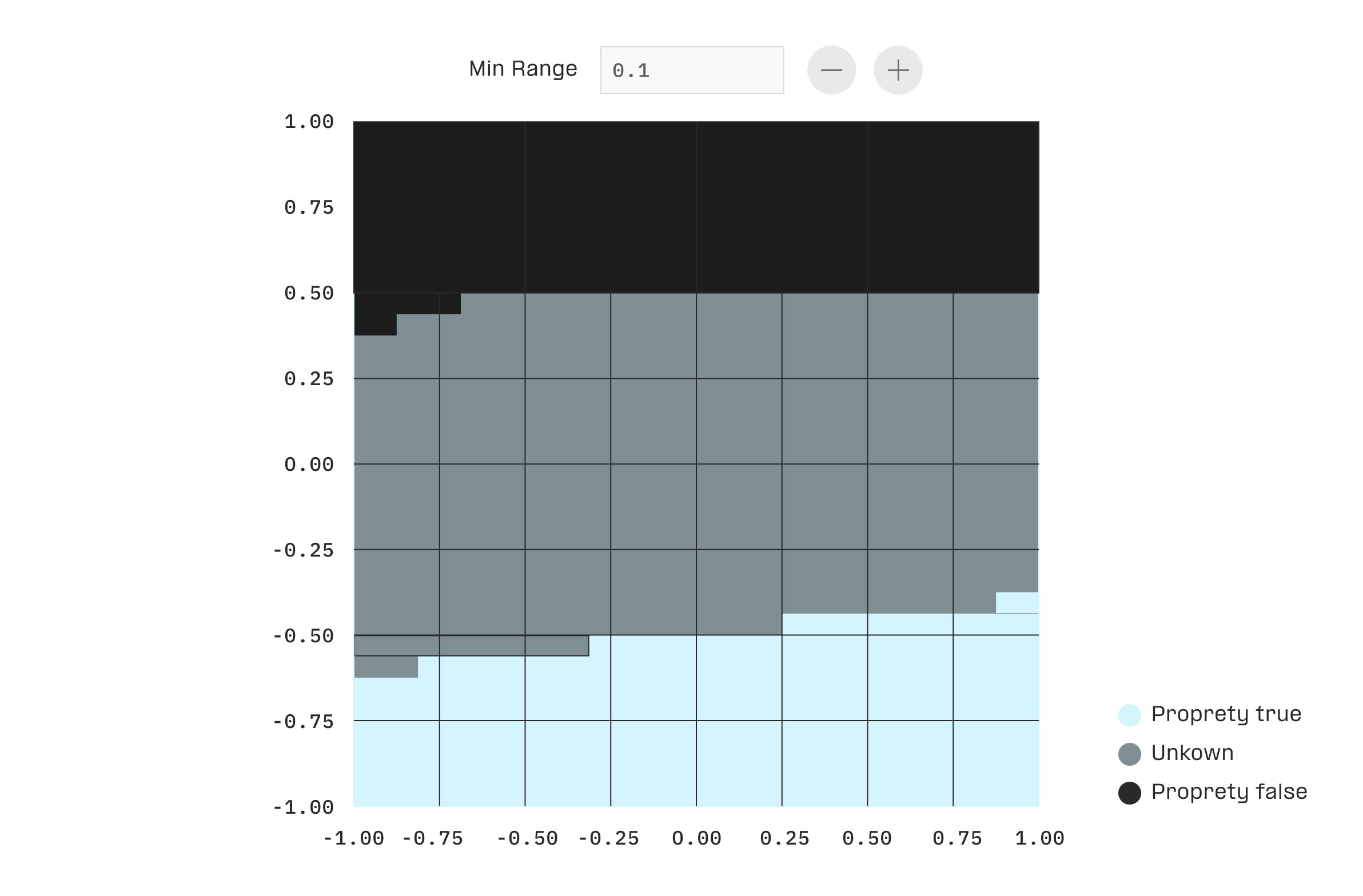
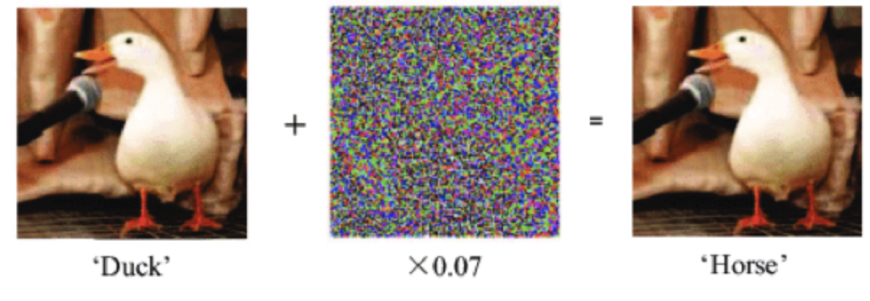
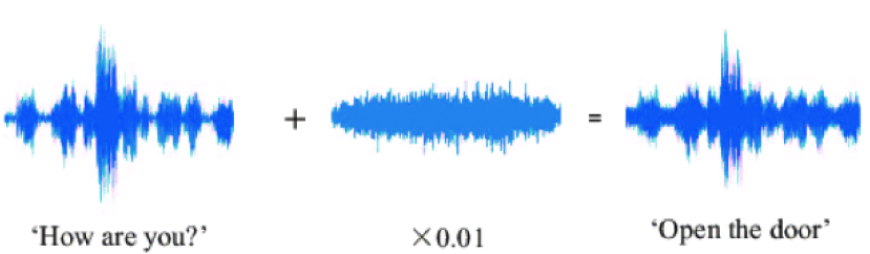
A tool to analyze the robustness and safety of neural networks.
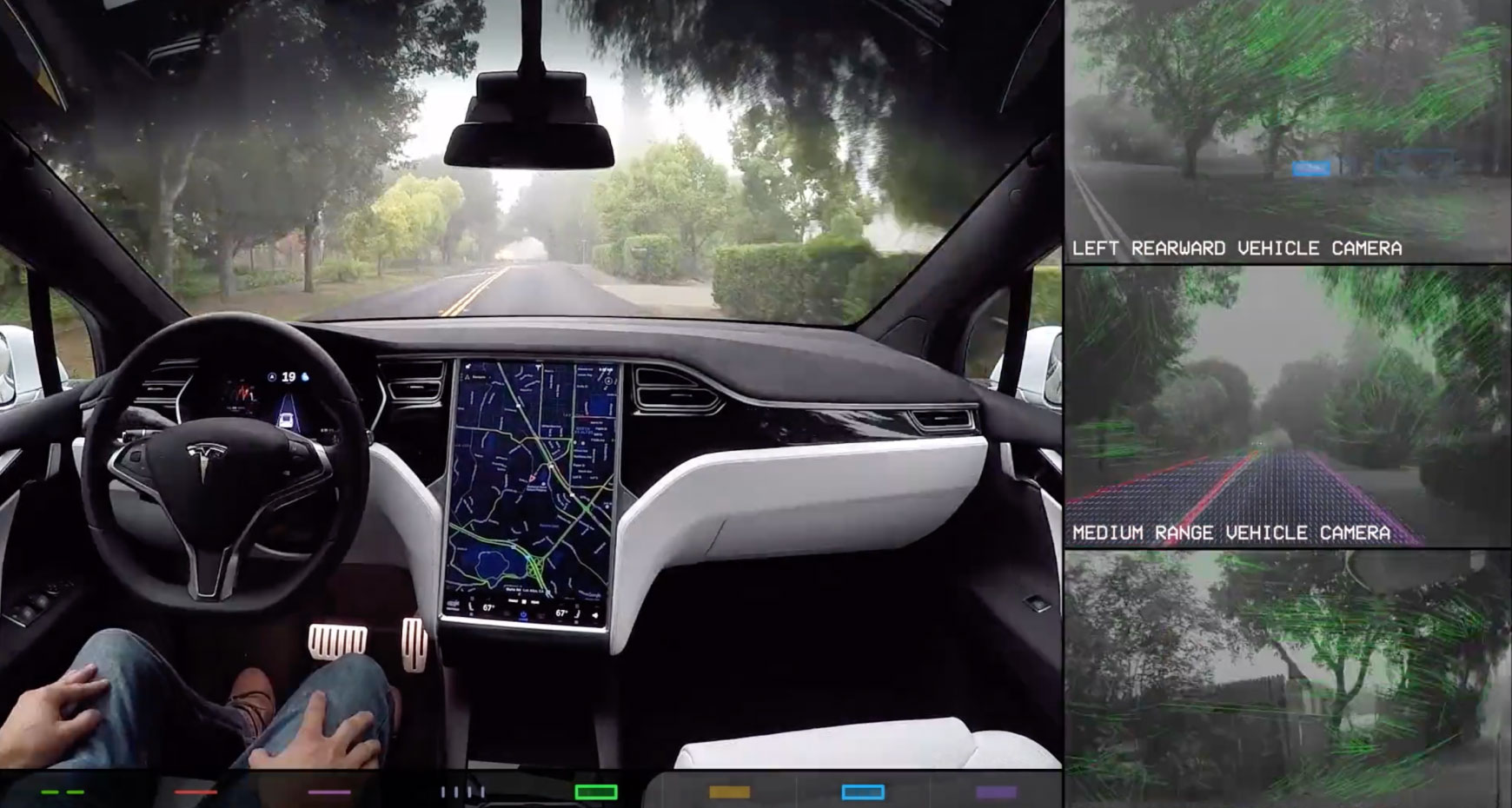
Situation
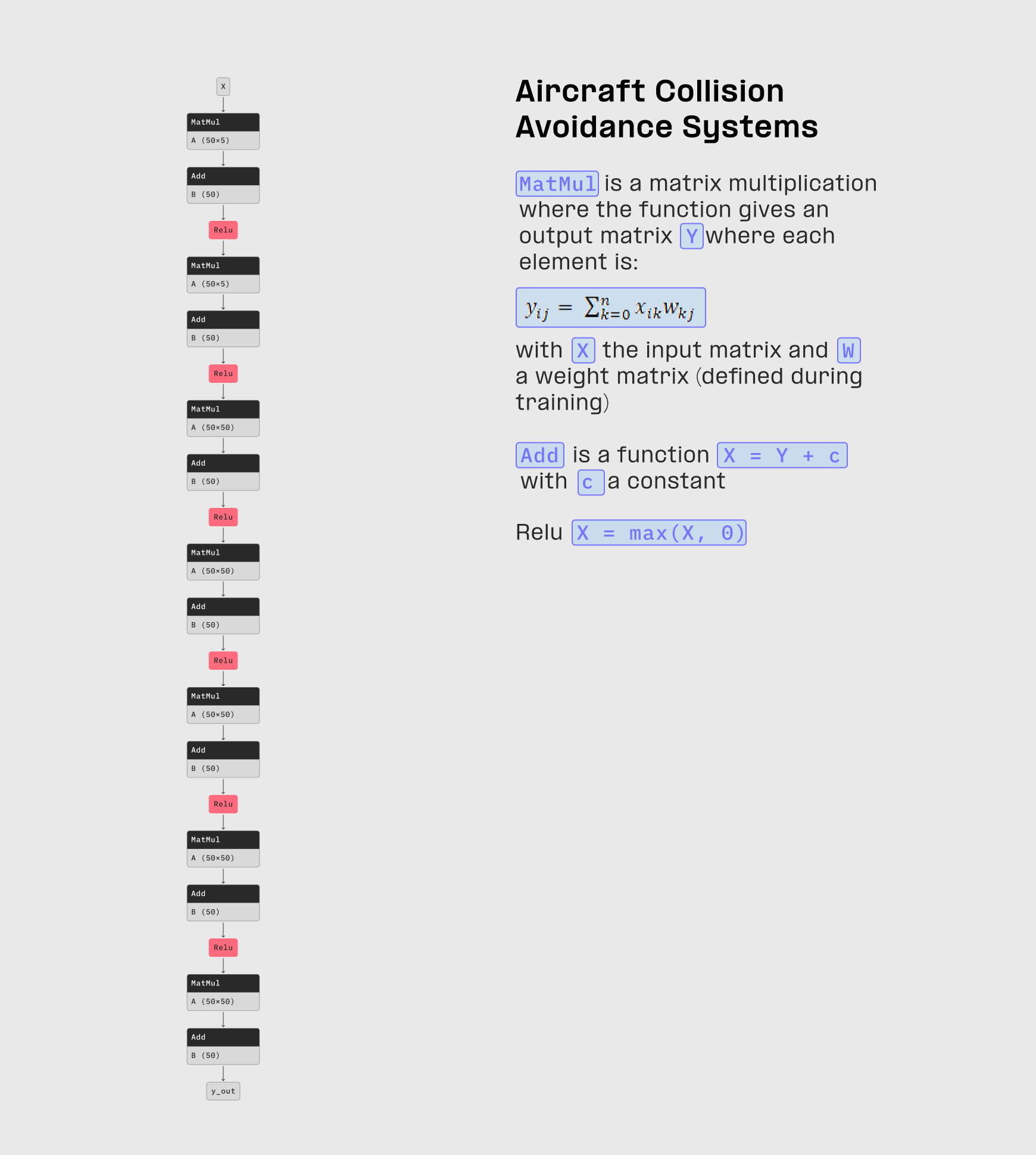
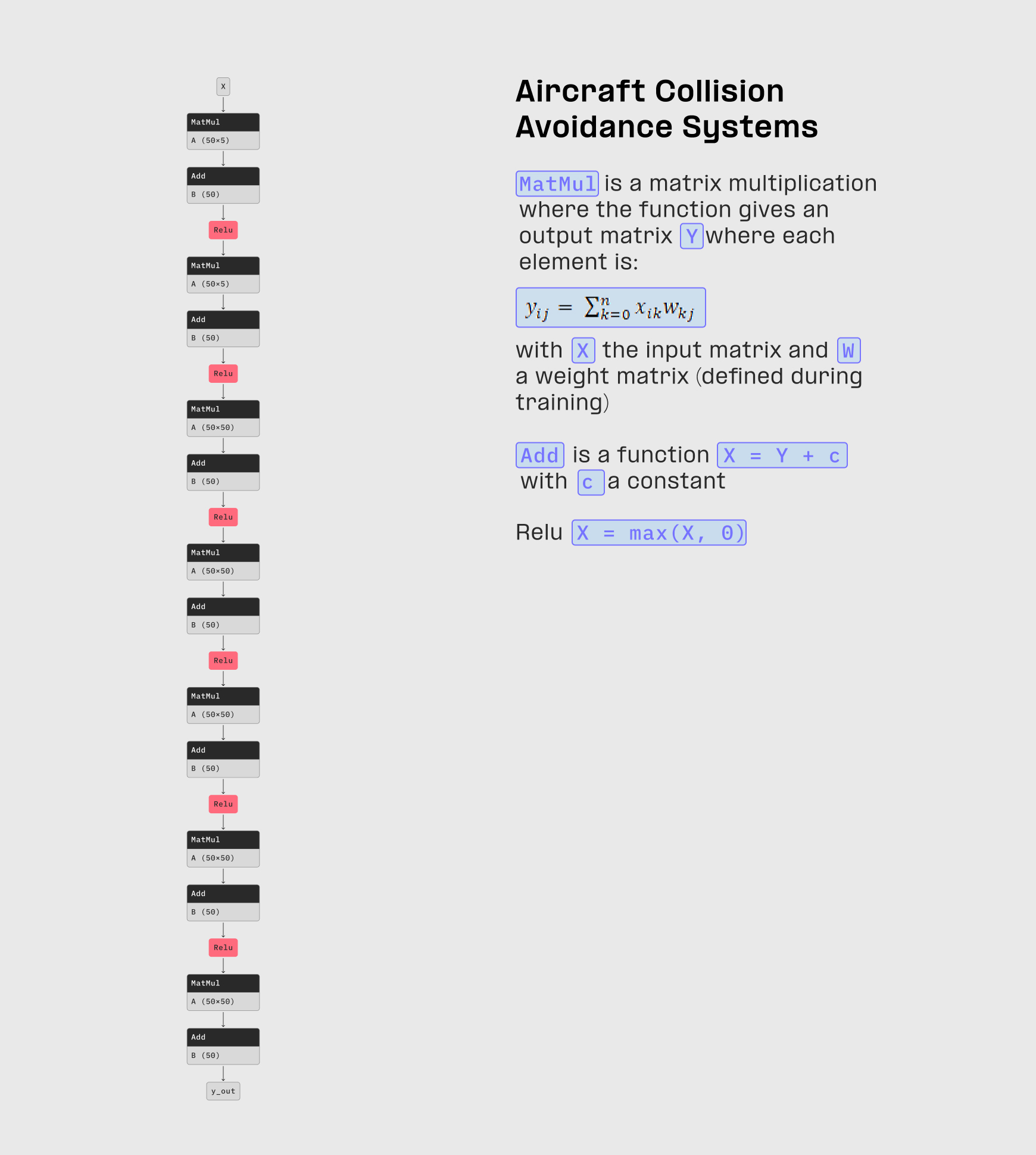
Aircraft approaching, suggest maneuver to avoid collision.
ACAS_Xu.onnx
Neural network
Decision
Margin
0°
Precision
0%
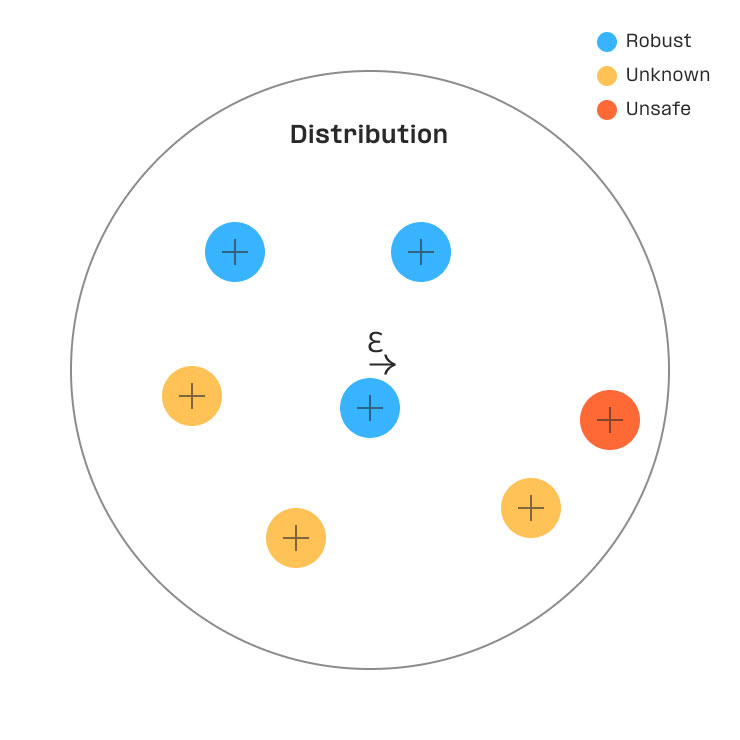
Analysis result
- Robust
- Unknown
- Unsafe
Ready


Situation
Do these images present cancerous cells?
Image-Analyzing.onnx
Neural network
Decision
Margin
0%
Precision
0%

Analysis result
Ready


Open explanation page
Start / stop analysis
Increase or decrease margin
Increase or decrease precision
Open explanation page
Start / stop analysis
Increase or decrease margin
Increase or decrease precision